Graph Heuristics - Intro | Emperor of A101

What is a graph?

not the coordinate plane graph
represents a network of relationships between objects

Components

Nodes/Vertices
Edges
- Nodes are connected with edges

alt text /

Representating a Graph

To work with graphs, we need to represent them in code. There are three common ways to do this.

Node and Edge Sets
- List of Nodes (in this case JGraphT calls them Vertices)
- List of Edges
  - Each edge is represented by the two nodes it is connected to
Adjacency Matrix
- N x N matrix, where N is the number of nodes
- Column and Row for each node
- 1 represents an edge between node and column of cell
- 0 represents no connected between node and column of cell
Adjacency List
- LinkedList or Dictionary (python)
- 1 key for every node
- Each key’s value is a list of all the nodes it is connected to

%maven org.jgrapht:jgrapht-core:1.5.1

import org.jgrapht.*;
import org.jgrapht.graph.*;
import org.jgrapht.generate.*;
import org.jgrapht.util.SupplierUtil;

import java.util.*;
import java.util.function.Supplier;

Supplier<String> vSupplier = new Supplier<>() {
    private int id = 0;
    public String get() { return "" + id++; }
};

Graph<String, DefaultEdge> g = new SimpleGraph<>(vSupplier, SupplierUtil.createDefaultEdgeSupplier(), false);

GnmRandomGraphGenerator<String, DefaultEdge> generator = new GnmRandomGraphGenerator<>(10, 15);
generator.generateGraph(g);

System.out.println("Vertices: " + g.vertexSet());
System.out.println("Edges: " + g.edgeSet());

List<String> vertices = new ArrayList<>(g.vertexSet());
Collections.sort(vertices);

System.out.println("\nAdjacency Matrix:");
System.out.print("  ");
for (String v : vertices) {
    System.out.print(v + " ");
}
System.out.println();

for (String v1 : vertices) {
    System.out.print(v1 + " ");
    for (String v2 : vertices) {
        boolean connected = g.containsEdge(v1, v2);
        System.out.print((connected ? 1 : 0) + " ");
    }
    System.out.println();
}

System.out.println("\nAdjacency List:");
for (String v : vertices) {
    Set<DefaultEdge> edges = g.edgesOf(v);
    List<String> neighbors = new ArrayList<>();
    for (DefaultEdge e : edges) {
        String src = g.getEdgeSource(e);
        String tgt = g.getEdgeTarget(e);
        if (src.equals(v)) {
            neighbors.add(tgt);
        } else {
            neighbors.add(src);
        }
    }
    Collections.sort(neighbors);
    System.out.println(v + ": " + neighbors);
}

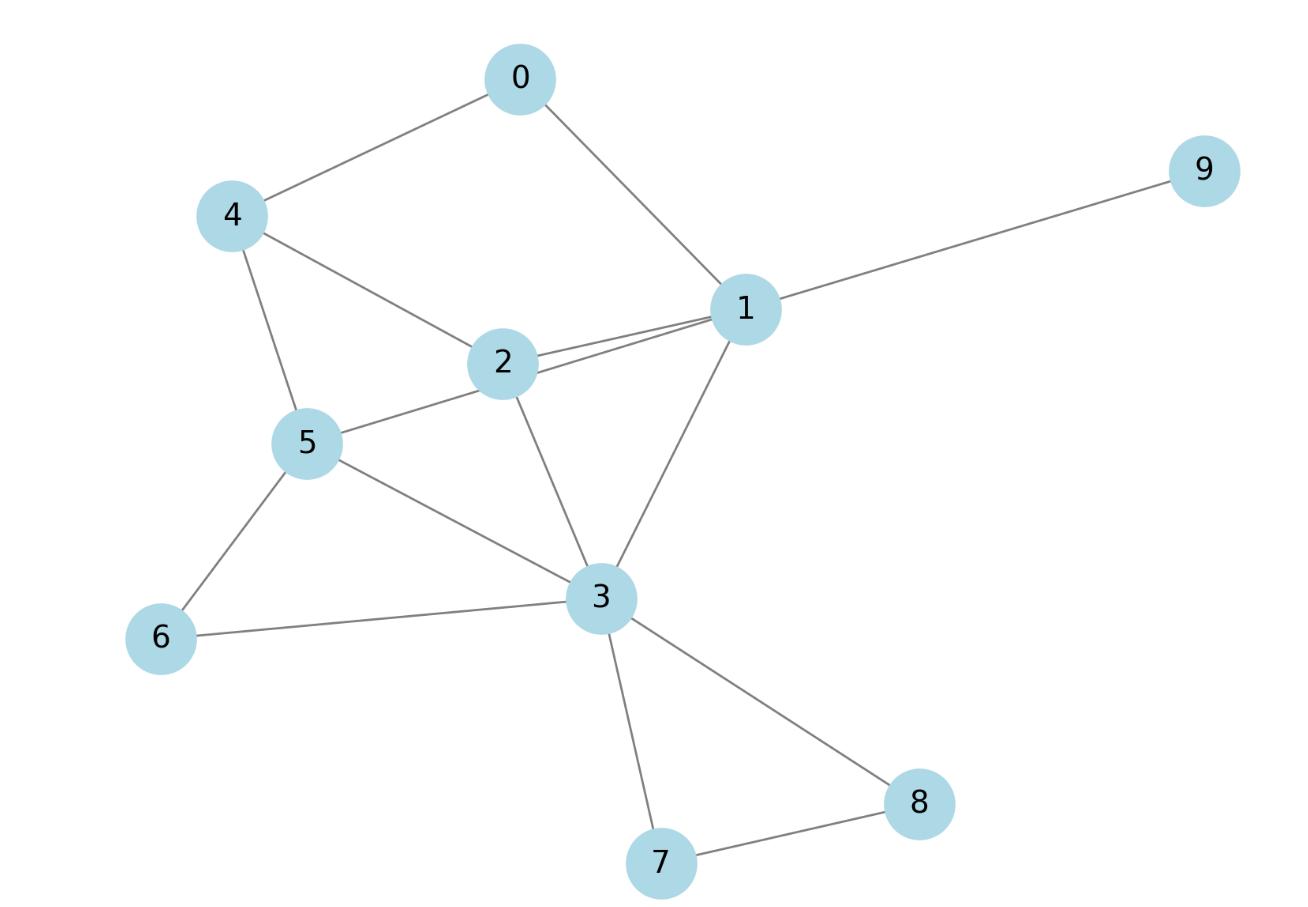
Vertices: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Edges: [(3 : 5), (8 : 7), (7 : 3), (2 : 4), (3 : 1), (0 : 1), (4 : 5), (1 : 2), (8 : 3), (6 : 3), (5 : 6), (5 : 1), (2 : 3), (4 : 0), (1 : 9)]

Adjacency Matrix:
1 2 3 4 5 6 7 8 9 
0 1 0 0 1 0 0 0 0 0 
1 0 1 1 0 1 0 0 0 1 
0 1 0 1 1 0 0 0 0 0 
0 1 1 0 0 1 1 1 1 0 
1 0 1 0 0 1 0 0 0 0 
0 1 0 1 1 0 1 0 0 0 
0 0 0 1 0 1 0 0 0 0 
0 0 0 1 0 0 0 0 1 0 
0 0 0 1 0 0 0 1 0 0 
0 1 0 0 0 0 0 0 0 0 

Adjacency List:
[1, 4]
[0, 2, 3, 5, 9]
[1, 3, 4]
[1, 2, 5, 6, 7, 8]
[0, 2, 5]
[1, 3, 4, 6]
[3, 5]
[3, 8]
[3, 7]
[1]

Popcorn Hack #1

Which of the three representations above is most efficient?

The adjacency list, because unlike the matrix it only stores the information that is necessary rather than storing the n^2 amount with having all the empty/nonexistent connections.

Types of Graphs

Weighted

In a Weighted Graph, each node is assigned a cost, a number representing cost to traverse that edge. The total cost is the sum of the costs of all nodes traveled. Weighted graphs are useful where traveling between different nodes is less or more prefereable.

Directed

In a directed Graph, each node can only be traveled in one direction.

Real Applications

Traveling Salesman Problem
- Salesman must travel to every city to sell his products. He wants to do so in least possible time
- City = Node
- Path between Cities = Edge
- Weighted by time it takes to travel between cities
- Hamiltonian Path/Cycle: path must visit each node exactly once

Homework Part 1

How might I represented a weighted graph?
- Using an Adjacency List?
- Using a Vertex and Edge Set?

Answer: A weighted graph can be represented with an adjacency list by having each list be a list of pairs of weights and the node name. So if we wanted to to show that node A has a connection to node B with a weight of 5, the list for node A might be [("B", 5)]. Using a vertex and edge set, your vertex list would be the same but your edge set would not just store the two nodes of the edge but also the weight (so it would have vertex1, vertex2, and the edge weight).

How might I represented a directed graph?
- Using an Adjacency List?
- Using a Vertex and Edge Set?

Answer: A directed graph can be represented the same way as an undirected graph both as an adjacency list or a vertex and edge set. However, the difference is that you will not always have the edges in both directions. So rather than having two lists for each edge in both directions, you will only have the edge be for one direction.

Represent the following graph using an adjacency matrix

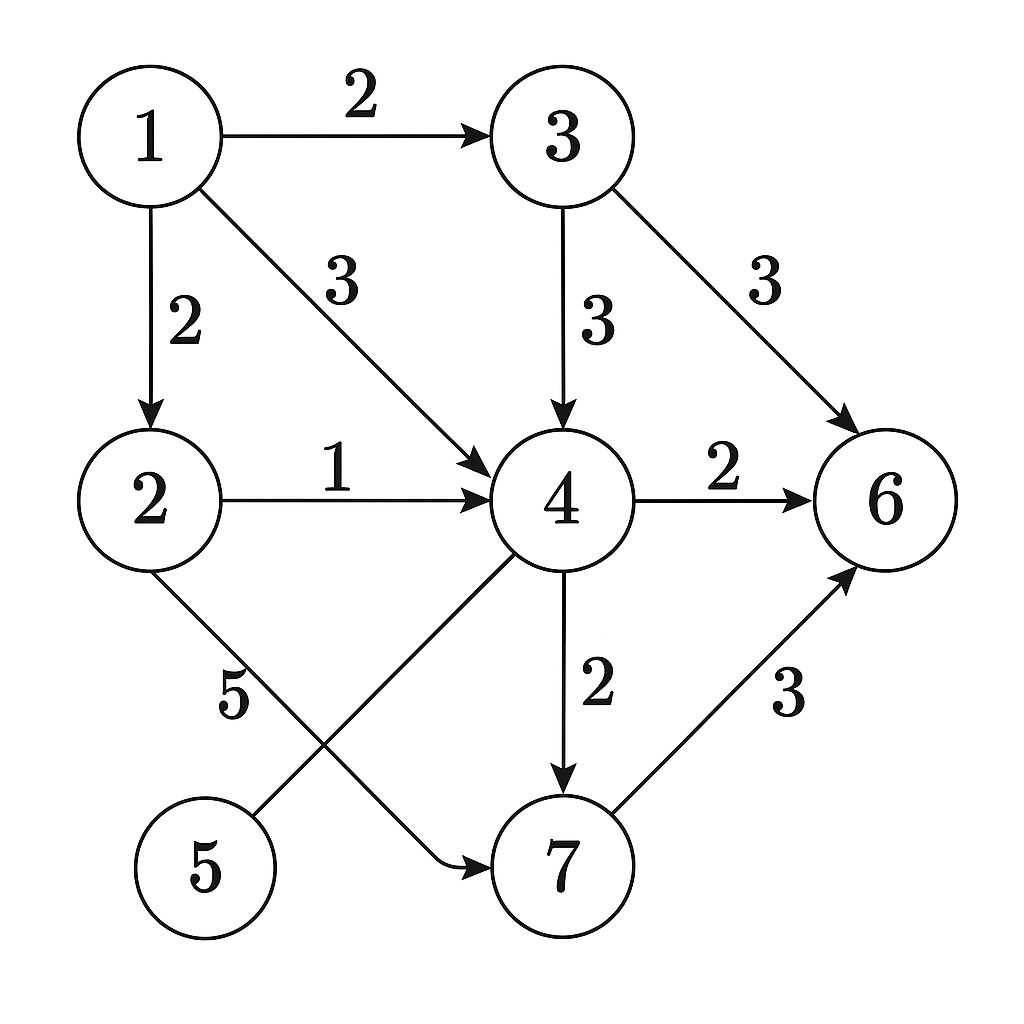
Answer:

2  3  4  5  6  7
0  2  2  3  0  0  0
0  0  0  1  0  0  5
0  0  0  3  0  3  0
0  0  0  0  0  2  2
0  0  0  0  0  0  0
0  0  0  0  0  0  0
0  0  0  0  0  3  0